Sayısal (Lojik) Devrelerden Boolean İfadesinin Elde Edilmesi

Bir lojik ifade yani boolean ifadesi verildiğinde bu ifade sayısal (lojik) devreye dönüştürülebilir.  Aynı şekilde lojik devrelerden de sayısal ifadeleri elde edebiliriz.  Aşağıdaki  lojik devrelerden boolean ifadesinin elde edilmesi ile ilgili örnekler yer almaktadır.

Kaynak:https://immibbilisim.com/moduller/4-%20Temel%20Mant%C4%B1k%20Devreleri.pdf

Devamını oku

Boolean İfadesinden Sayısal Devrelerin Çizilmesi

Bir lojik ifadeden sayısal bir devre çizmek olduk basit bir işlemdir. Verilen lojik ifade için sayısal devre doğrudan çizilebilir ya da lojik ifade sadeleştirilip (karnaugh haritası ya da başka bir yöntemle) daha sonra sayısal devre çizilir.

örnek 1:   D=B+AC lojik ifadesini lojik kapılar kullanarak çiziniz.

örnek 2:  Y= A + B.C denkleminin lojik kapılı devresini çiziniz.

örnek 3: Y = [(A + B).C] + D denkleminin lojik kapılı devresini çiziniz.

Aşağıdaki eğitim videosunda boolean ifadesinden sayısal devrelerin çizimi ile ilgili çözümlü örnekler yer almaktadır.

Aşağıdaki videosunda ise sayısal devrelerden boolean ifadesinin çıkarılması ile ilgili çözümlü örnekler yer almaktadır.

Kaynaklar :

https://320volt.com/istanbul-teknik-universitesi-lojik-devre-tasarimi-soru-cevaplari/
https://immibbilisim.com/moduller/4-%20Temel%20Mant%C4%B1k%20Devreleri.pdf

Devamını oku

Boolean Matematiği (Boolean Theorems)

Boolean matematiği, sayısal (lojik) devrelerin tasarım ve analizinde kullanılır.  Boolean matematiği ikilik sayı sistemi düzenine dayanır ve işlemler ikilik sayılara göre yapılır. İkilik sayılarda lojik 0 ve lojik 1 kullanılır.

Boolean matematiğinde toplama , çıkarma, çarpma ve bölme işlemleri aynen uygulanır ve aşağıdaki tabloya göre çeşitli işlemler gerçekleştirilir.

Boolean Matematiğinde Hesaplamalar :Boolean matematiğinde dört çeşit hesap vardır. Bunlar Ve (.), Veya (+), Değil (‘) ve son olarak Özel Veya (Å). 

Boolean matematiği temel kurallar : 

Ve (.)	0 . 0 = 0	0 . 1 = 0	1 . 0 = 0	1 . 1 = 1
Veya (+)	0 + 0 = 0	0 + 1 = 1	1 + 0 = 1	1 + 1 = 1
Değil (‘)	0 ‘ = 1		1 ‘ = 0

Formüller	0 Değeri Verildiğinde	1 Değeri Verildiğinde
A . 0 = 0	A = 0 ise, 0 . 0 = 0	A = 1 ise, 1 . 0 = 0
A . 1 = A	A = 0 ise, 0 . 1 = 0	A = 1 ise, 1 . 1 = 1
A + 0 = A	A = 0 ise, 0 + 0 = 0	A = 1 ise, 1 + 0 = 1
A + 1 = A	A = 0 ise, 0 + 1 = 1	A = 1 ise, 1 + 1 = 1
A . A = A	A = 0 ise, 0 . 0 = 0	A = 1 ise, 1 . 1 = 1
A + A = A	A = 0 ise, 0 + 0 = 0	A = 1 ise, 1 + 1 = 1
A . A’ = 0	A = 0 ise, 0 . 1 = 0	A = 1 ise, 1 . 0 = 0
A + A’ = 1	A = 0 ise, 0 + 1 = 1	A = 1 ise, 1 + 0 = 1
(A’)’ = A	A = 0 ise, A’ = 1, (A’)’ = 0	A = 1 ise, A’ = 0, (A’)’ =

Boolean matematiğinde önemli bir kanun ise de morgan teoremidir. De morgan teoremi bazı karmaşık ifadelerin sadeleştirilmesinde önemli katkı sağlar. De morgan teoreminin iki önemli kuralı aşağıdaki gibidir.

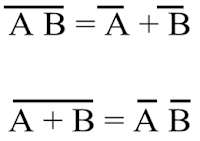-de morgan theorem-

kaynaklar: https://diyot.net/boolean-matematigi/

Devamını oku