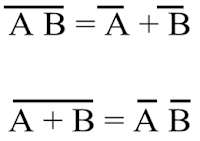Boolean İfadesinden Sayısal Devrelerin Çizilmesi

Bir lojik ifadeden sayısal bir devre çizmek olduk basit bir işlemdir. Verilen lojik ifade için sayısal devre doğrudan çizilebilir ya da lojik ifade sadeleştirilip (karnaugh haritası ya da başka bir yöntemle) daha sonra sayısal devre çizilir.

örnek 1:   D=B+AC lojik ifadesini lojik kapılar kullanarak çiziniz.

örnek 2:  Y= A + B.C denkleminin lojik kapılı devresini çiziniz.

örnek 3: Y = [(A + B).C] + D denkleminin lojik kapılı devresini çiziniz.

Aşağıdaki eğitim videosunda boolean ifadesinden sayısal devrelerin çizimi ile ilgili çözümlü örnekler yer almaktadır.

Aşağıdaki videosunda ise sayısal devrelerden boolean ifadesinin çıkarılması ile ilgili çözümlü örnekler yer almaktadır.

Kaynaklar :

https://320volt.com/istanbul-teknik-universitesi-lojik-devre-tasarimi-soru-cevaplari/
https://immibbilisim.com/moduller/4-%20Temel%20Mant%C4%B1k%20Devreleri.pdf

Devamını oku

Proteus Kurulumu (Proteus Setup)

Proteus programını www.labcenter.com adresinden indirilip kurulumu yapılabilir.  Bu sitede proteus programı için iki seçenek mevcuttur. Programın tam sürümü satın alınabilir ya da proteusun demo versiyonu siteden indirilebilir.

Proteus programı İSİS ve ARES olmak üzere iki kısma ayrılır. İsiste , elektronik devre kurulumu ve simülasyonu gerçekleştirilir. Ares arayüzünde ise İsis de kurulan devrelerin baskı devre görünümü çıkarılır.

Proteus (İsis ve Ares) programının kurulum aşamalarını aşağıdaki videodan izleyebilirsiniz.

Elektrik-Elektronik-Robotik-Kodlama eğitimlerini şu linke tıklayarak ÜCRETSİZ izleyebilirsiniz youtube.com/elektronikderslerimizle


Aşağıda pek çok ders ve alanda ücretsiz eğitim setleri yer almaktadır:

-DEVRE ANALİZİ 1 Eğitim Setimiz                        ►►https://goo.gl/gLkn7D
-DEVRE ANALİZİ 2 Eğitim Setimiz                        ►►https://goo.gl/jdh2M1
-DİJİTAL ELEKTRONİK (LOJİK) Eğitim Setimiz  ►►https://goo.gl/VWIocN
-PİC PROGRAMLAMA Eğitim Setimiz                   ►►https://goo.gl/S0nvAh
-PROTEUS Eğitim Setimiz                                        ►►https://goo.gl/VchPln
-BASKI DEVRE Eğitim Setimiz                               ►►https://goo.gl/SqlPUu
-OHM Kanunu Eğitim Setimiz                                   ►►https://goo.gl/H5achb

Devamını oku

Boolean Matematiği (Boolean Theorems)

Boolean matematiği, sayısal (lojik) devrelerin tasarım ve analizinde kullanılır.  Boolean matematiği ikilik sayı sistemi düzenine dayanır ve işlemler ikilik sayılara göre yapılır. İkilik sayılarda lojik 0 ve lojik 1 kullanılır.

Boolean matematiğinde toplama , çıkarma, çarpma ve bölme işlemleri aynen uygulanır ve aşağıdaki tabloya göre çeşitli işlemler gerçekleştirilir.

Boolean Matematiğinde Hesaplamalar :Boolean matematiğinde dört çeşit hesap vardır. Bunlar Ve (.), Veya (+), Değil (‘) ve son olarak Özel Veya (Å). 

Boolean matematiği temel kurallar : 

Ve (.)	0 . 0 = 0	0 . 1 = 0	1 . 0 = 0	1 . 1 = 1
Veya (+)	0 + 0 = 0	0 + 1 = 1	1 + 0 = 1	1 + 1 = 1
Değil (‘)	0 ‘ = 1		1 ‘ = 0

Formüller	0 Değeri Verildiğinde	1 Değeri Verildiğinde
A . 0 = 0	A = 0 ise, 0 . 0 = 0	A = 1 ise, 1 . 0 = 0
A . 1 = A	A = 0 ise, 0 . 1 = 0	A = 1 ise, 1 . 1 = 1
A + 0 = A	A = 0 ise, 0 + 0 = 0	A = 1 ise, 1 + 0 = 1
A + 1 = A	A = 0 ise, 0 + 1 = 1	A = 1 ise, 1 + 1 = 1
A . A = A	A = 0 ise, 0 . 0 = 0	A = 1 ise, 1 . 1 = 1
A + A = A	A = 0 ise, 0 + 0 = 0	A = 1 ise, 1 + 1 = 1
A . A’ = 0	A = 0 ise, 0 . 1 = 0	A = 1 ise, 1 . 0 = 0
A + A’ = 1	A = 0 ise, 0 + 1 = 1	A = 1 ise, 1 + 0 = 1
(A’)’ = A	A = 0 ise, A’ = 1, (A’)’ = 0	A = 1 ise, A’ = 0, (A’)’ =

Boolean matematiğinde önemli bir kanun ise de morgan teoremidir. De morgan teoremi bazı karmaşık ifadelerin sadeleştirilmesinde önemli katkı sağlar. De morgan teoreminin iki önemli kuralı aşağıdaki gibidir.

-de morgan theorem-

kaynaklar: https://diyot.net/boolean-matematigi/

Devamını oku