Sayısal (lojik) bir devrede verilen bir problemi çözmek için belli adımların bilinmesi gerekir. Yani belirli kurallar problemi çözmek için temel teşkil etmektedir. Sayısal devre tasarımında girişler ve çıkışlar vardır ve verilen girişlere göre çıkış değerleri değişmektedir.
"Örneğin, 4 adet sensör bulunan bir sistemde sensörlerden en az iki tanesi aktif olduğunda çıkıştaki motoru çalıştıran bir devre tasarlayınız." Bu şekilde bir soruyu çözmek için aşağıdaki adımlar izlenir:
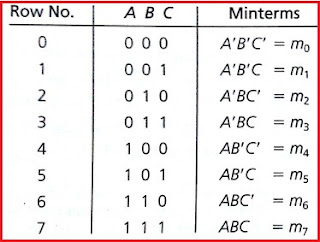
Öncelikle verilen sistem için doğruluk tablosu oluşturulur.
Oluşturulan doğruluk tablosuna göre giriş çıkış değerleri oluşturulur.
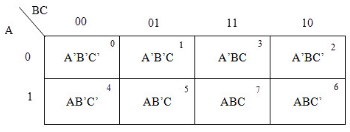
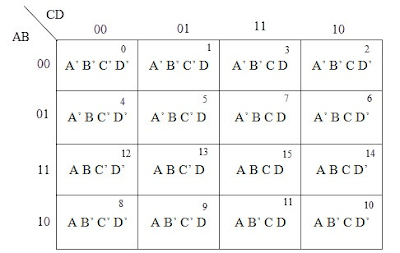
Doğruluk tablosuna göre karno haritaları oluşturulur.
Karno haritaları çıkış değerleri belirlenir.
Son olarak çıkış değerlerine göre lojik devre çizimi gerçekleştirilir.
Aşağıdaki videolarda sayısal tasarım ile ilgili örnek soru çözümleri yapımıştır.
Karnaugh haritaları (kmaps) sayısal elektronik (lojik) alanında önemli bir yer tutmaktadır. Lojik ifadeler karno haritaları kullanılarak kolay bir şekilde sadeleştirilebilir. Çok karmaşık boolean ifadelerini karno haritaları ile sadeleştirmek mümkündür.
Karno haritaları hazırlanırken giriş sayıları dikkate alınır. Örneğin 3 girişli bir lojik ifade için 2 üzeri 3=8 li karno haritası kullanılır.
2 giriş için 4
3 giriş için 8
4 giriş için 16
5 giriş için 32 li karno haritası oluşturulur.
Aşağıdaki şekilde 4 girişli bir karno haritası yer almaktadır. Dolayısıyla 16 lı bir karnaugh haritası oluşturulmuştur.
karnaugh haritası
Örneğin, A=B+CD ifadesi basit bir boolean ifadesidir. Zaten sade bir ifadedir. Bu ifade daha fazla sadeleştirilemez . Dolayısıyla bu ifadede karno haritalarını kullanmak gereksizdir. Fakat Q=ABC+ABC'+AB'C+A'BC gibi bir ifade için karno haritaları kullanılabilir. Çünkü bu ifadeyi sadeleştirmek zordur. Dolayısıyla 3 girişimiz (A,B,C) olduğundan 8 li bir karno haritası oluşturabiliriz.
2 değişkenli karnaugh haritası : Bu kutu tipi dijital devrede iki tane giriş olduğu zaman kullanılır. Ayrıca karnaugh haritası 2^2 =4 adet kutucuğa sahiptir.
-2 değişkenli karno haritası-
3 değişkenli karnaugh haritası :Bu kutu tipi dijital devrede üç tane giriş olduğu zaman kullanılır. Ayrıca karnaugh haritası 2^3 =8 adet kutucuğa sahiptir.
-3 değişkenli karno haritası-
4 değişkenli karnaugh haritası : Bu kutu tipi dijital devrede dört tane giriş olduğu zaman kullanılır. Ayrıca karnaugh haritası 2^4 =16 adet kutucuğa sahiptir.
-4 değişkenli karnaugh haritası-
Karnaugh Haritalarında Gruplama Nasıl Yapılır ?
Karnaugh Haritaları giriş değişkeni sayısına bağlı olarak standart sayıda kutudan oluşur.
n=giriş değişkeni sayısı olmak üzere 2n formülüyle kutu sayısı belirlenir. 2,4,8,16… olmak üzere 2‟ye katlanarak devam eder.
Karnaugh Haritalarında hedef ençok “1” i gruplamaktır. Kutuların içindeki “1” ler dikkate alınır. Boş olan kutu “0” demektir, dikkate alınmaz.
Gruplamalardaki kutu sayısı 1,2,4,8,16…. şeklinde olmalıdır.
Her bir grup çıkış ifadesinde giriş değişkenleri çarpım (AND) şeklinde ifade edilir.
Birden fazla gruba sahip Karnaugh Haritasının çıkış ifadesinde gruplar toplama (OR) işlemine tabi tutulur.
Karnaugh Haritasında tüm kutular “1” ise çıkış “1” , tüm kutular “0” ise çıkış “0” dır.
Aşağıda karno haritalarında doğru ve yanlış gruplandırma örnekleri yer almaktadır.
Aşağıdaki video eğitimlerinde karno haritaları anlatılmıştır ve karnaugh haritaları ile ilgili sorular yer almaktadır.
Maxtermleri lojik ifadelerin toplamlarının çarpımı olarak özetleyebiliriz.
Aşağıdaki örnekte 3 girişli bir tablo hazırlanmıştır. Girişlere göre çıkış ifadesi lojik 0 ve lojik 1 değerini almıştır. Bizden istenen lojik 0 değerine göre işlem yapmaktır.
-maxterm-
Aşağıdaki video derste maxtermler (toplamların çarpımı) ile ilgili örnekler yer almaktadır.
